function_AnisSect_explorer  |
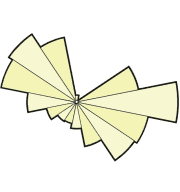  |  |
Visualization of anisotropic supports
Shows the anisotropic neighborhoods (i.e. union of the supports of the adaptive-scale kernels) which are used for estimation in the Anisotropic LPA-ICI algorithms. |
|
demo_CreateLPAKernels
utility_DrawLPAKernels |
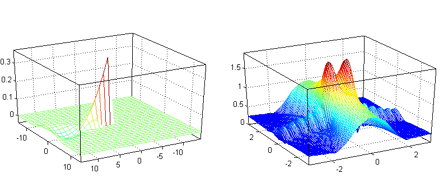 | 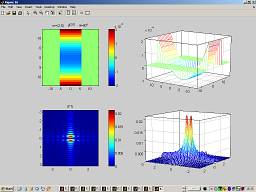 |
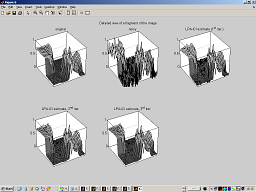
LPA kernel design
Creates LPA kernels and draws them. |
|
| demo_DenoisingGaussian |
 | 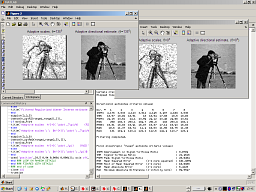 |
Anisotropic LPA-ICI denoising
Performs the Anisotropic LPA-ICI denoising on observations which are contaminated by additive Gaussian white noise. |
|
| demo_RecursiveDenoisingGaussian |
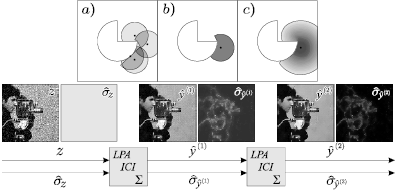 |  |
Recursive Anisotropic LPA-ICI denoising
Performs the recursive Anisotropic LPA-ICI denoising on observations which are contaminated by additive Gaussian white noise. |
|
| demo_DeblurringGaussian |
 | 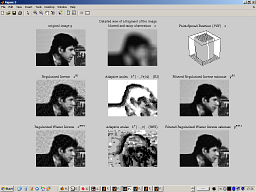 |
Anisotropic LPA-ICI deconvolution
Performs deblurring (deconvolution) from observations which are blurred and noisy. The RI (Regularized Inverse) and RWI (Regularized Wiener Inverse) Deconvolution Algorithm with Anisotropic LPA-ICI adaptive estimate selection is used. |
|
| demo_DenoisingSignDepNoise |
 |  |
Recursive Anisotropic LPA-ICI denoising for Signal-Dependent Noise
Performs the recursive Anisotropic LPA-ICI denoising on observations which are contaminated by signal-dependent noise (e.g. Poisson, Film-Grain, Speckle). |
|
| demo_DeblurringPoissonian |
  |  |
Anisotropic LPA-ICI Poissonian Deconvolution
Performs deblurring (deconvolution) from observations which are blurred and noisy. Noise is modeled as a Poisson process. |
|
| demo_InverseHalftoning |
 | 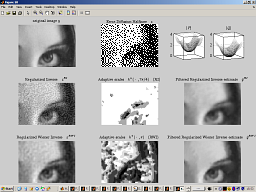 |
Anisotropic LPA-ICI Inverse-Halftoning
Reconstructs a continuous-tone image from a given error-diffusion halftone image. Inverse-halftoning is performed using the Anisotropic LPA-ICI deconvolution with RI (regularized inverse) and RWI (regularized Wiener inverse) adaptive-scale estimates. |
|
| demo_AnisotropicGradient |
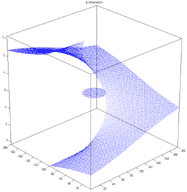  | 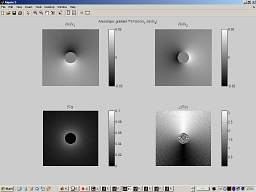 |
| Demonstrates the Anisotropic Gradient concept using the Riemann surface example. |
|
| demo_CreateMRLPAKernels |
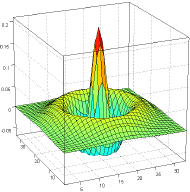 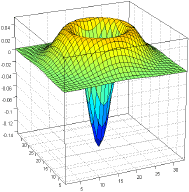 | 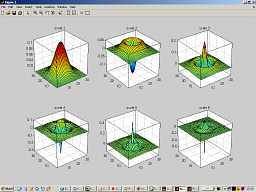 |
Multiresolution LPA kernel design
Creates and draws multiresolution (MR) LPA two-dimensional kernels. |
|
| demo_MR_FilteringGaussian |
  | 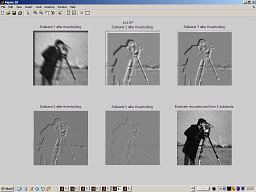 |
Anisotropic multiresolution (MR) LPA Denoising
Performs the MR anisotropic LPA denoising on observations which are contaminated by additive Gaussian white noise. Multiscale kernels are used for MR signal analysis and thresholding for noise removal. |
 .
.



























