 |
| TRANSFORMATIONS | REFERENCES |
| Transformations |
 Information and instructions |
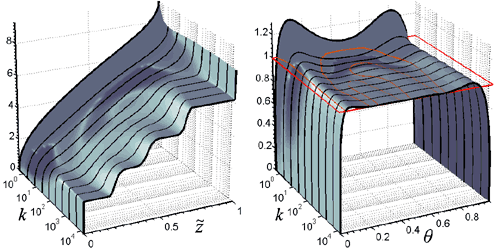
Optimized variance-stabilizing transformations 8-Mbyte zip-file includes Matlab MAT-file (ver. 5 or later) and 16-digit ASCII (double precision) formats released July 1, 2009 | 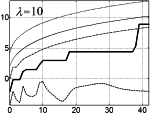 |
 before you proceed with downloading any of the files.
before you proceed with downloading any of the files.
| References |
 Foi, A., “Optimization of variance-stabilizing transformations”, preprint, 2009.
Foi, A., “Optimization of variance-stabilizing transformations”, preprint, 2009.